Graph Search

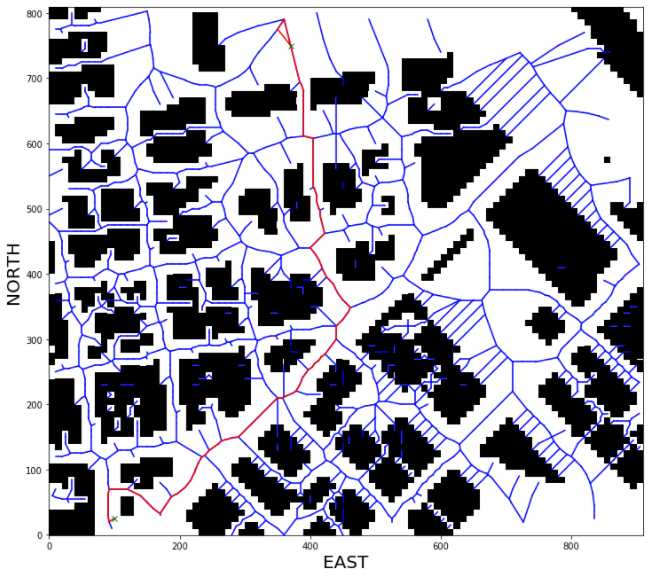
Alright now things are getting interesting! You've got a couple different methods for building a graph, and you've got some tools you developed previously to search through grids. You may have started to notice that grids and graphs actually have a lot in common, and with the medial axis transform in particular, we're really sort of straddling the divide between grids and graphs.

The fact is that grids are really just a subset of graphs where all possible actions are of a fixed size and direction. Graphs on the other hand, are more flexible and allow you to define actions over any distance and in any direction. These similarities mean that you can take your grid-based search methods and easily modify them to work on a graph!

Graph-based A*

In the last two exercises you generated graph representations of your search space. The way A* worked for a grid was that in expanding your list of partial plans, you considered the sum of the cost function G and the heuristic H in deciding where to move to next.

For graphs-based A*, you'll do essentially the same thing. The "Manhattan distance" as a heuristic no longer makes sense, but Euclidean distance can still serve as a perfectly valid heuristic estimate. For the cost function, you can now think of the cost of moving between two nodes as a function of the distance between those nodes in the graph. And with that, you have your graph-based A* implementation!

NetworkX

In order to make graph creation and manipulation simple, we're going to leverage a powerful package called NetworkX. With Networkx, it's easy to take the nodes and edges you found using the Voronoi and medial axis methods and arrange them into a single graph object. In this exercise you'll start with the Voronoi method to extract a graph where nodes and edges don't collide with obstacles. Then you'll use NetworkX to build up a graph object like this:

# Assuming you have already extracted "edges"
# And edges is a list of tuples of the form (p1, p2)
import networkx as nx

G = nx.Graph()
for e in edges:
    p1 = e[0]
    p2 = e[1]
    dist = LA.norm(np.array(p2) - np.array(p1))
    G.add_edge(p1, p2, weight=dist)